Sự ra đời của DeepSeekMath-V2, do DeepSeek phát triển, đã tạo ra một bước ngoặt đáng chú ý. Mô hình này không chỉ giải được các bài toán ở cấp độ cao nhất, mà còn cho thấy AI có thể lập luận toán học một cách minh bạch. Hãy cùng tìm hiểu về mô hình toán học này trong bài viết dưới đây!
1. Năng lực lập luận toán học của DeepSeekMath-V2
1.1 Vì sao IMO, CMO và Putnam được xem là “đỉnh cao” của toán học?
Các kỳ thi như Olympic Toán học Quốc tế (IMO), Olympic Toán học Trung Quốc (CMO) hay Putnam từ lâu đã được coi là chuẩn mực cao nhất để đánh giá năng lực tư duy toán học. Đây không đơn thuần là những bài kiểm tra kiến thức, mà là nơi đánh giá khả năng trừu tượng hóa vấn đề, xây dựng lập luận nhiều tầng và trình bày lời giải với độ chính xác tuyệt đối. Ngay cả những thí sinh đoạt huy chương vàng cũng thường trải qua nhiều năm huấn luyện chuyên sâu.
1.2 Thành tích cụ thể của DeepSeekMath-V2 tại các kỳ thi hàn lâm
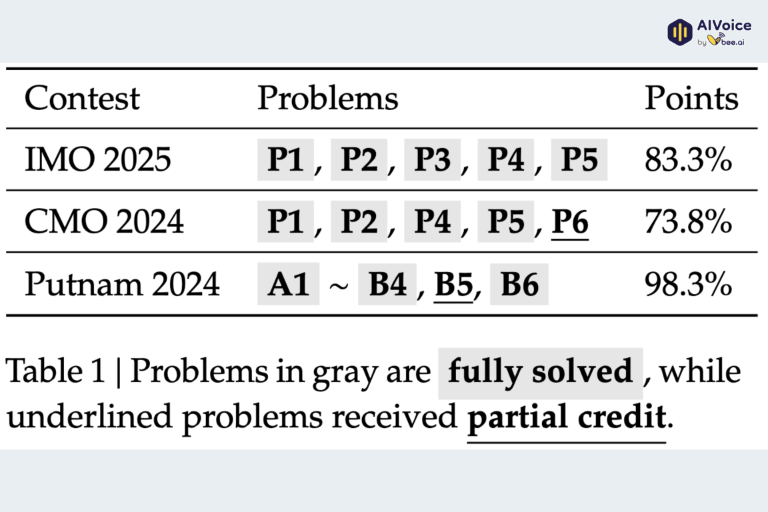
Trong bối cảnh đó, thành tích của DeepSeekMath-V2 tạo ra sự chú ý đặc biệt. Tại IMO 2025, mô hình giải đúng 5 trên 6 bài toán, đạt mức điểm tương đương huy chương vàng. Điều quan trọng không chỉ nằm ở số lượng bài giải, mà ở việc mô hình xử lý tốt các bài yêu cầu chứng minh phức tạp, vốn là dạng bài khó nhất ngay cả với thí sinh hàng đầu.
Trước đó, tại CMO 2024, DeepSeekMath-V2 tiếp tục đạt chuẩn huy chương vàng theo hệ thống chấm điểm chính thức, cho thấy khả năng duy trì hiệu suất ổn định. Đặc biệt, trong kỳ thi Putnam 2024 nổi tiếng với độ khó cực cao, mô hình đạt 118 trên 120 điểm, vượt xa kỷ lục 90 điểm cao nhất mà con người từng đạt được trong lịch sử cuộc thi.
2. Tối ưu kiến trúc tự kiểm chứng của DeepSeekMath-V2
Trong nhiều năm, một trong những điểm yếu lớn nhất của các mô hình AI khi giải toán là hiện tượng “đáp án đúng nhưng lập luận sai”. Do được huấn luyện để tối ưu xác suất sinh ra văn bản có vẻ hợp lý, các mô hình ngôn ngữ lớn thường tạo ra những chuỗi suy luận nghe hợp lý nhưng thực chất chứa lỗi logic, bỏ qua bước trung gian hoặc dựa trên giả định ngầm không hợp lệ.
DeepSeekMath-V2 giải quyết tận gốc vấn đề trên bằng cách tách biệt rõ ràng giữa quá trình tạo lập luận và quá trình kiểm chứng. Trong kiến trúc Generator–Verifier, Proof Generator đóng vai trò như một nhà toán học sáng tạo, đề xuất giả thuyết và xây dựng chuỗi lập luận ban đầu. Những lập luận này không cần hoàn hảo, mà được xem như các phương án khả thi.
Song song với đó, Proof Verifier hoạt động như một người phản biện nghiêm khắc, kiểm tra từng bước suy luận để phát hiện lỗi logic, mâu thuẫn hoặc bước nhảy thiếu cơ sở. Nếu phát hiện sai sót, Verifier yêu cầu Generator suy luận lại.
Quy trình này được lặp lại nhiều vòng cho đến khi toàn bộ chuỗi lập luận đạt độ chặt chẽ cao nhất. Nhờ đó, DeepSeekMath-V2 không chỉ đưa ra đáp án đúng, mà còn đảm bảo rằng con đường dẫn đến đáp án đó hoàn toàn minh bạch và phù hợp với tiêu chuẩn học thuật.
3. Cách DeepSeekMath-V2 tư duy như một nhà toán học thực thụ
3.1 Chiến lược đa hướng giải cho các bài toán phức tạp
Đối với những bài toán có độ phức tạp cao, DeepSeekMath-V2 không giới hạn mình trong một hướng suy nghĩ duy nhất. Mô hình có thể tạo ra nhiều hướng giải song song, sau đó đánh giá và lựa chọn phương án có độ tin cậy cao nhất. Cách tiếp cận này mô phỏng quá trình làm việc của một nhóm nhà toán học cùng tranh luận và phản biện.

3.2 Lập luận hoàn toàn bằng ngôn ngữ tự nhiên
Một điểm đặc biệt quan trọng là DeepSeekMath-V2 không sử dụng bất kỳ công cụ hỗ trợ bên ngoài nào như máy tính hay trình thông dịch mã. Toàn bộ quá trình giải toán được thực hiện bằng ngôn ngữ tự nhiên, thông qua lập luận logic thuần túy. Điều này giúp mô hình tiến gần hơn đến cách con người suy nghĩ và chứng minh toán học.
4. So sánh các phiên bản DeepSeekMath
Để hiểu rõ hơn về sự tiến bộ vượt bậc của DeepSeekMath-V2, chúng ta hãy so sánh nó với phiên bản tiền nhiệm:
| Tiêu chí | DeepSeekMath-V1 | DeepSeekMath-V2 |
| Thời gian ra mắt | Tháng 2/2024 | Tháng 11/2025 |
| Quy mô tham số | 7B (7 tỷ) | 685B (685 tỷ) |
| Nền tảng mô hình | DeepSeek-Coder-v1.5 7B | DeepSeek-V3.2-Exp-Base |
| Dữ liệu huấn luyện | 500B tokens (120B math tokens) | Chuyên sâu về toán học + proof-based RL |
| Kiến trúc đặc biệt | GRPO (Group Relative Policy Optimization) | Generator-Verifier với tự kiểm chứng |
| Cơ chế xác minh | Không có | Có (Proof Verifier) |
| Hiệu suất MATH benchmark | 51.7% (base), ~60% (RL) | Không công bố cụ thể |
| IMO 2025 | Chưa có dữ liệu | 5/6 bài (~83.3%) – Huy chương vàng |
| CMO 2024 | Chưa có dữ liệu | Đạt chuẩn huy chương vàng |
| Putnam 2024 | Chưa có dữ liệu | 118/120 điểm (kỷ lục) |
| Hỗ trợ công cụ | Có | Không cần |
| Yêu cầu phần cứng | GPU 16GB+ VRAM | GPU 40GB+ VRAM (hoặc quantized) |
| Điểm mạnh | Nhỏ gọn, dễ triển khai, hỗ trợ tool | Độ chính xác cao, tự kiểm chứng, hiệu suất đỉnh cao |
| Giấy phép | MIT License + Model License | Apache 2.0 |
DeepSeekMath-V2 không chỉ đơn thuần là phiên bản nâng cấp về quy mô, mà là một bước nhảy vọt về triết lý thiết kế. Trong khi V1 tập trung vào việc tối ưu hóa hiệu suất với kích thước nhỏ gọn và khả năng sử dụng công cụ bên ngoài, V2 hướng đến việc tạo ra một “nhà toán học AI” thực thụ có khả năng tự suy luận, tự kiểm tra và tự tin vào kết quả của mình mà không cần sự trợ giúp từ bên ngoài.

5. So sánh DeepSeekMath-V2 với các mô hình AI khác
| Tiêu chí | DeepSeekMath-V2 | OpenAI o3 | OpenAI o4-mini | Gemini Deep Think | Claude Opus 4 | GPT-4.5/5 |
| Nhà phát triển | DeepSeek (Trung Quốc) | OpenAI (Mỹ) | OpenAI (Mỹ) | Google DeepMind (Mỹ) | Anthropic (Mỹ) | OpenAI (Mỹ) |
| Thời gian công bố | Tháng 11/2025 | Tháng 12/2024 | Tháng 6/2025 | Tháng 7/2025 | 2025 | 2025 |
| Quy mô | 685B parameters | ~671B (ước tính) | Nhỏ hơn (~70B) | Chưa công bố | Chưa công bố | Chưa công bố |
| Cơ chế đặc biệt | Generator-Verifier tự kiểm chứng | Suy luận sâu nội bộ | Suy luận gọn, tối ưu tốc độ | Suy luận rất sâu + song song | Chế độ suy nghĩ mở rộng | Suy luận linh hoạt theo ngữ cảnh |
| Thời gian suy luận | Chưa công bố | Có thể lâu nếu bài toán phức tạp | Nhanh, hiệu quả | 4.5 giờ (IMO) | Vài giây – vài phút | ~2-10+ giây |
| Công cụ hỗ trợ | Không cần (tự suy luận) | Có | Có | Có | Có | Có |
| Giá API (ước tính) | Cạnh tranh (chưa công bố) | $3-15 input / $15-75 output | Rẻ hơn 63% so với o3-mini | $1.25-2.50 / $5-10 | $3-15 / $15-75 | $2 / $8 |
| Điểm mạnh nổi bật | • Putnam xuất sắc • Tự kiểm chứng • Mã nguồn mở | • FrontierMath dẫn đầu • AIME xuất sắc • Suy luận rất sâu | • AIME 2025 tốt nhất • Chi phí thấp • Nhanh | • IMO chính thức • ICPC vàng • Ngôn ngữ tự nhiên | • Suy nghĩ, đào sâu vấn đề • SWE-bench 72.7% | • Linh hoạt • Hệ sinh thái trưởng thành |
| Hạn chế | • Chi phí tính toán cao • Cần GPU mạnh • Mới ra mắt | • Không mã nguồn mở • Chi phí cao • Có độ trễ | • Nhỏ hơn o3 • Ít chuyên sâu toán | • Không mã nguồn mở • Cần huấn luyện riêng | • Không mã nguồn mở • Chi phí cao | • Không mã nguồn mở • Ít chuyên sâu toán |
Qua bảng có thể thấy, DeepSeekMath-V2 nổi bật như một mô hình chuyên sâu về toán học và suy luận logic, khác với các mô hình AI đa năng như GPT-4.5/5 hay Claude Opus vốn thiên về ứng dụng và sản phẩm. Điểm mạnh cốt lõi của DeepSeekMath-V2 là khả năng tự kiểm chứng lời giải và mã nguồn mở, rất phù hợp cho nghiên cứu, giáo dục và các bài toán chứng minh phức tạp.
6. Công nghệ đằng sau thành công của DeepSeekMath-V2
Thành tích vượt trội của DeepSeekMath-V2 không đến từ một cải tiến đơn lẻ, mà là kết quả của sự kết hợp giữa quy mô mô hình rất lớn, kiến trúc tối ưu cho lập luận dài và phương pháp huấn luyện được thiết kế chuyên biệt cho chứng minh toán học.

6.1 Quy mô mô hình và kiến trúc tính toán
DeepSeekMath-V2 được xây dựng trên nền tảng DeepSeek-V3.2-Exp-Base, một mô hình có quy mô thuộc hàng lớn nhất hiện nay. Với khoảng 685 tỷ tham số, mô hình sở hữu năng lực biểu diễn rất cao, cho phép nắm bắt những cấu trúc logic phức tạp thường xuất hiện trong các bài toán chứng minh dài và nhiều tầng suy luận.
Bên cạnh quy mô, mô hình còn sử dụng linh hoạt nhiều định dạng số học khác nhau như BF16, F8_E4M3 và F32. Việc kết hợp này giúp cân bằng giữa độ chính xác số học và hiệu suất tính toán, đặc biệt quan trọng khi xử lý các chuỗi lập luận dài, nơi sai số nhỏ có thể lan truyền và phá vỡ toàn bộ chứng minh.
Một điểm đáng chú ý khác là việc áp dụng cơ chế Sparse attention (Chú ý thưa). Thay vì tính toán toàn bộ mối quan hệ giữa mọi token, mô hình chỉ tập trung vào những phần thông tin thực sự liên quan trong từng giai đoạn suy luận. Nhờ đó, DeepSeekMath-V2 có thể xử lý các chứng minh toán học rất dài mà vẫn giữ được hiệu quả tính toán và độ ổn định của lập luận.
6.2 Phương pháp huấn luyện hướng tới lập luận sâu
Không giống các mô hình ngôn ngữ được huấn luyện chủ yếu để sinh văn bản tự nhiên, DeepSeekMath-V2 trải qua một quy trình huấn luyện nhiều giai đoạn, được thiết kế riêng cho tư duy toán học.
- Ở giai đoạn đầu, mô hình học từ các tài liệu toán học chuyên sâu, bao gồm sách giáo khoa, bài giảng và các chứng minh chuẩn mực. Giai đoạn này giúp mô hình hình thành nền tảng về cấu trúc và ngôn ngữ của lập luận toán học.
- Tiếp theo, mô hình được thực hành với các bài toán tổng hợp, nơi nhiều khái niệm và kỹ thuật được kết hợp trong cùng một lời giải. Đây là bước chuyển quan trọng từ việc “nhận diện mẫu” sang việc xây dựng chuỗi suy luận có mục tiêu.
- Điểm then chốt nằm ở giai đoạn học tăng cường dựa trên chứng minh (proof-based reinforcement learning). Trong giai đoạn này, mô hình không chỉ tạo ra lời giải mà còn được đánh giá bởi một cơ chế xác minh nội bộ. Cách thiết kế này buộc mô hình phải ưu tiên những suy luận chính xác và có chiều sâu, thay vì những lời giải ngắn nhưng thiếu nền tảng logic.
7. Ý nghĩa và tiềm năng ứng dụng dài hạn
7.1 Đặt nền móng cho AI đáng tin cậy hơn
Cơ chế suy luận tự kiểm chứng của DeepSeekMath-V2 không chỉ mang ý nghĩa trong toán học. Quan trọng hơn, nó mở ra một hướng tiếp cận mới cho việc xây dựng AI có thể giải thích và bảo vệ quyết định của chính mình. Khi AI có khả năng tự kiểm tra lập luận, mức độ minh bạch và độ tin cậy của hệ thống sẽ được nâng lên đáng kể.
Điều này có thể trở thành một tiêu chuẩn mới cho các ứng dụng AI trong thế giới thực, nơi “kết quả đúng” là chưa đủ, mà còn cần hiểu rõ vì sao kết quả đó đúng.

7.2 Tiềm năng ứng dụng trong các lĩnh vực trọng yếu
- Phát triển phần mềm và lập trình: Những mô hình có khả năng lập luận và tự kiểm chứng có thể không chỉ viết mã, mà còn phân tích và chứng minh tính đúng đắn của chương trình. Điều này giúp giảm thiểu các lỗi nghiêm trọng, đặc biệt trong những hệ thống lớn và phức tạp, đồng thời nâng cao chất lượng và độ an toàn của mã nguồn.
- Nghiên cứu khoa học: Khả năng tự động kiểm chứng các chuỗi lý luận phức tạp mở ra tiềm năng hỗ trợ xây dựng và đánh giá giả thuyết khoa học. Với toán học, đây thậm chí còn có thể là bước tiến hướng tới việc hỗ trợ chứng minh các định lý mới, hoặc ít nhất là kiểm tra tính hợp lệ của những chứng minh dài và khó.
- Y tế, tài chính hay pháp lý: Việc AI có thể giải thích rõ ràng logic đằng sau quyết định của mình là yếu tố then chốt để đảm bảo an toàn và trách nhiệm. Một hệ thống AI biết tự kiểm chứng sẽ đáng tin cậy hơn nhiều so với những mô hình chỉ đưa ra kết quả mà không thể giải thích.
- Giáo dục: DeepSeekMath-V2 cho thấy tiềm năng trở thành một công cụ học tập mạnh mẽ. Thay vì chỉ cung cấp đáp án, mô hình có thể trình bày toàn bộ quá trình giải một cách logic và chi tiết, giúp học sinh và sinh viên hiểu sâu bản chất của bài toán. Điều này đặc biệt có giá trị trong việc dạy và học toán học ở trình độ cao.
8. Xu hướng tương lai của AI toán học
Qua DeepSeekMath-V2, có thể thấy rõ một trong những hướng phát triển chính của AI toán học nói riêng và các mô hình trí tuệ nhân tạo nói chung: khả năng tự học và tự cải tiến.
Thay vì chỉ dựa vào dữ liệu huấn luyện ban đầu, các mô hình AI thế hệ mới sẽ:
- Học hỏi từ các tác vụ thực tế.
- Tự điều chỉnh thuật toán để đạt hiệu suất tốt hơn.
- Phát triển khả năng tự kiểm chứng và sửa lỗi.
- Tiến gần hơn đến việc xây dựng hệ thống AI tổng quát (AGI).
Với AI ngày càng mạnh mẽ, việc đảm bảo chúng được sử dụng một cách có trách nhiệm trở nên vô cùng quan trọng. Điều này đòi hỏi con người phải xây dựng bộ quy tắc, tiêu chuẩn đạo đức và khuôn khổ pháp lý rõ ràng hơn để quản lý và khai thác tiềm năng của công nghệ này một cách an toàn và có lợi cho toàn xã hội.

9. Câu hỏi thường gặp về DeepSeekMath-V2
9.1 Có thể sử dụng DeepSeekMath-V2 miễn phí không?
Có, DeepSeek cung cấp nhiều cách để sử dụng mô hình này miễn phí:
- Giao diện web: Truy cập chat.deepseek.com để sử dụng trực tiếp.
- Mã nguồn mở: Tải về từ Hugging Face hoặc GitHub theo giấy phép Apache 2.0.
- API: DeepSeek cũng cung cấp API với chi phí cạnh tranh cho các ứng dụng thương mại.
9.2 DeepSeekMath-V2 có thể giải quyết những loại bài toán nào?
Mô hình này có khả năng xử lý đa dạng các bài toán toán học từ cơ bản đến nâng cao:
- Đại số (phương trình, bất phương trình, hệ phương trình).
- Hình học (chứng minh hình học, tính toán diện tích, thể tích).
- Giải tích (giới hạn, đạo hàm, tích phân).
- Lý thuyết số (số nguyên tố, chia hết, đồng dư).
- Tổ hợp và xác suất.
- Các bài toán Olympic toán học quốc tế.
9.3 Làm thế nào để biết lời giải của AI là đúng?
Đây chính là điểm mạnh của DeepSeekMath-V2. Mô hình sử dụng cơ chế tự kiểm chứng qua hai thành phần:
- Proof Generator tạo lời giải.
- Proof Verifier kiểm tra từng bước lập luận.
Nếu phát hiện sai sót, hệ thống sẽ tự động yêu cầu tạo lời giải mới. Quá trình này lặp lại cho đến khi đảm bảo chuỗi lập luận hoàn toàn chính xác. Người dùng có thể đọc từng bước giải để hiểu rõ logic và tự kiểm chứng.
9.4 Có cần kiến thức lập trình để sử dụng DeepSeekMath-V2 không?
Không nhất thiết phải biết kiến thức lập trình để sử dụng DeepSeekMath-V2.
- Người dùng thông thường: Có thể sử dụng qua giao diện web chat.deepseek.com mà không cần biết lập trình.
- Nhà phát triển: Nếu muốn tích hợp vào ứng dụng hoặc tùy chỉnh mô hình, cần có kiến thức về Python và các thư viện Machine learning (Học máy).
9.5 DeepSeekMath-V2 có hỗ trợ tiếng Việt không?
Mô hình chủ yếu được huấn luyện trên dữ liệu tiếng Anh và tiếng Trung, nhưng có khả năng hiểu và trả lời bằng tiếng Việt ở mức độ nhất định. Tuy nhiên, để đạt kết quả tốt nhất khi giải toán, nên:
- Diễn đạt bài toán rõ ràng bằng tiếng Việt hoặc tiếng Anh.
- Sử dụng ký hiệu toán học chuẩn quốc tế.
- Có thể kết hợp với công cụ dịch thuật nếu cần.
DeepSeekMath-V2 không chỉ đơn thuần là một mô hình AI giải toán giỏi. Đây là minh chứng cho một tầm nhìn mới về cách xây dựng hệ thống AI: không chỉ thông minh mà còn đáng tin cậy, không chỉ mạnh mẽ mà còn minh bạch trong quá trình tư duy. Với những gì DeepSeek đã đạt được, có thể khẳng định rằng cuộc đua phát triển khả năng lập luận của AI đang bước vào giai đoạn mới đầy hứa hẹn.

